Branch & Bound Tree

At the center of the branch & bound algorithm there are the Tree and Node classes. The Tree class can be customized to use user-provided branching and node selection strategies.

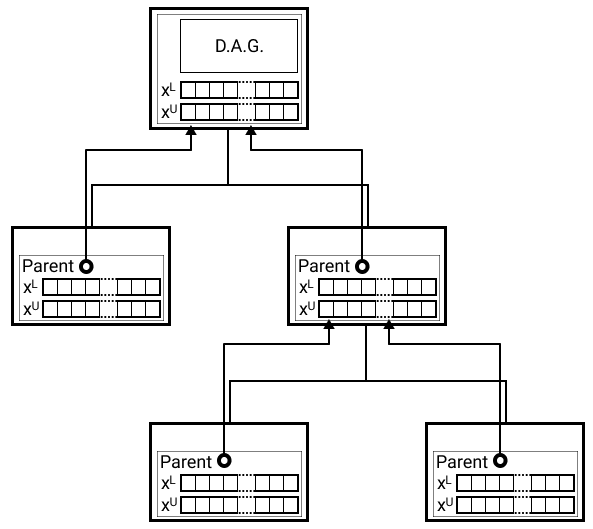
The Tree class is initialized with a root node that contains the original instance of the problem (with the original problem bounds). After solving the problem at the root node, the algorithm branches on one or more variables at one or more points to create multiple children nodes. The non-root nodes don’t store the entire problem, instead they only store the variables bounds at the node and a pointer to the parent problem.

The Branch & Bound Tree

When nodes are first created, they are marked as not visited and added to the queue of nodes to be visited. At each iteration of the branch & bound loop, the algorithm pops the most promising node from the queue and solves the node problem. The solution at the node is used to update the node state (global lower and upper bounds).

The tree upper bound is the best (lowest) feasible solution found so far, the function to update the tree upper bound is as follows:

def update_tree_upper_bound(tree, candidate_solution):
    if not candidate_solution.is_feasible:
        return

    tree.upper_bound = min(
        candidate_solution.objective_value,
        tree.upper_bound,
    )

The tree lower bound is the lowest of the open nodes lower bounds, that is the solution of the linear relaxation of the problem. Since open nodes have not been solved (by definition), then we consider their parent lower bound as their lower bound. If there are no open nodes, then we consider the lower bounds of phatomed nodes.

def update_tree_lower_bound(tree, candidate_solution):
    if not candidate_solution.is_feasible:
        return

    best_lower_bound = infinity
    for node in tree.open_nodes:
        node_lower_bound = node.parent.lower_bound
        if node_lower_bound < best_lower_bound:
            best_lower_bound = node_lower_bound

    if best_lower_bound != infinity:
        # The lower bound was updated from open nodes. Finished.
        tree.lower_bound = best_lower_bound
        return

    for node in tree.phatomed_nodes:
        node_lower_bound = node.parent.lower_bound
        if node_lower_bound < best_lower_bound:
            best_lower_bound = node_lower_bound

    # Update lower bound.
    tree.lower_bound = best_lower_bound